Data Analysis: T-TEST

This week we are going to talk about t-test. We use t-test to serve a few purposes but the two main things are comparing means of a continuous variable (e.g., GPA or income) with a categorical variable (e.g., gender or type of university--public vs. private)--that is called "independent group ttest," and comparing means between two continuous variables (e.g, pre-test and post-test)--that is called "paired t-test".

Independent Group T-Test

Research questions for this type of test may include: (1) are there any income differences between male and female employees? (2) Is GPA different by gender? (3) compared to those who have studied abroad, do those who have not earn more salary? (4) do people who went to a private university earn better salary compared to those who went to a public university? etc. Remember that t-test allows only two groups (e.g., male or female; study abroad vs. not study abroad). If you have a variable that has three or more groups (e.g., ethnicity or type of car etc.), then ANOVA (Oneway Analysis of Variance) is appropriate. We will cover this later. Let's look at our studentdata2008 data and try to run a few t-tests. First let's see if there is any difference in GPA between male and female students. The command for it is: ttest gpa, by(sexstud) . Note that the outcome variable (or dependent variable) is placed right after the command ttest and there is a "comma" sign after GPA, followed by "by" and the categorical variable in parenthesis.

Download studentdata2008 for your analysis below:

ttest gpa , by (sexstud) 

The first thing you are looking into at the above figure table is the mean values of female and male. It is clear that female scored higher on their GPA (6.58) compared to male of 5.68. Second, the probability value which in this case the middle one (the two-tailed test**see the notes below: for more information on this, this link to UCLA website is helpful). You are looking at a p value of less than 0.05 so that you can make a conclusion that there is a significant relationship between gender and GPA, specifically, to say that female is more likely to perform better than male. The circle #3 is used for your report write up. There are many ways you can write this up in your paper for your class or publication, but this is what I would write:

"This study seeks to examine the difference between academic performance by students' gender. The results based on an independent group t-test show that female students (M=6.58, SD=.13) tend to perform better than their male counterparts (M=5.68, SD=.14), t(268)=4.67, p<.001."

Note that whenever you report mean, you need to also report standard deviation.

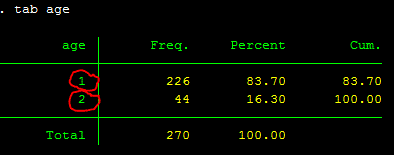
As you recall, last week we also use the command tab/sum to find the mean difference between two groups and it would give the same results to the ttest command. However, the tab/sum command does not give you statistical significance. So for example, if you run tab (sexstud), sum (gpa), you get the following:

tab (sexstud), sum (gpa)

You can see that the tab/sum command above gives you the same mean/sd results, but no statistical significance, and that's when t-test becomes useful.

So now how do you build a table that you can put it in your paper or report? You cannot copy and paste the ttest table above directly to your paper. Here it is a sample that I created for your reference:

If you have more than one variables, you can put them in after the academic performance, but their predictor (or Independent Variable) must be gender, otherwise, you need to create another table for it.

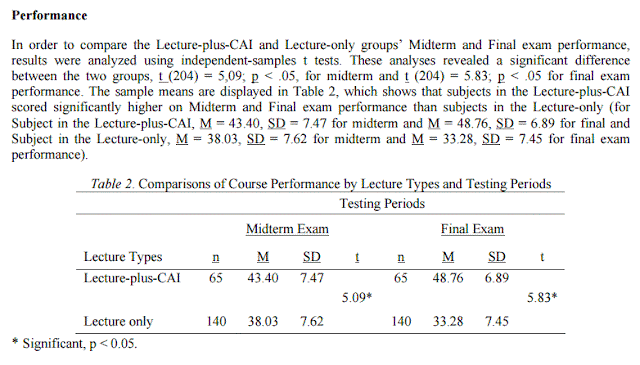
For your real world reference, I included below ttest results from an article published in Educational Technology & Society (pages 170-178) so that you can see the variety of tables are being used. It would be useful later when you become an evaluator of any program.

Paired T-Test 

This type of t-test seeks to answer relationship between two continuous variables that are not independent of one another, meaning that the same participants responded to the two variables at one point or two different times. For example, in my study, I compared involvement by mother and by father as reported by the student. So I have two measures: mother involvement and father involvement. I want to see the average scores of these two measures--which one scores higher? My hypothesis is that mother would have higher level of involvement than father. The command for this test is ttest involvemother==involvefather

Download studentdata2013 for your analysis below:

 ttest involvemother==involvefather 

Based on the above table, you can see that mother scored higher in their involvement with their children (M=2.52, SD=.67) compared to that of father (M=2.46, SD=.73), t(853)=3.37, p<.001.

Now it is your turn to practice your write up based on these above results as well as your APA styled table.

Paired-ttest is also commonly used for comparing scores from two different times, pre-test and post-test that are obtained from the same participants. Look at this report that my colleague, Dr. Scott Plunkett, Professor of Psychology at Cal State, Northridge and I wrote as part of an evaluation for Western Justice Center Foundation located in California, and how the results are reported and how the table is built (link to the report).

and this one:

and here is an excerpt taken from Executive Summary part of the report showing how the results were reported:

Practice on Your Own 

1. Using studentdata2013 data, please compare each involvement score between father and mother. In other words, is involvemom1 different from involvedad1 and so forth for the ten of them. Which one is significant?

2. Using studentdata2013 data, is there a difference between education of mother (edumom) in academic performance (rank) of their children?

3. Using studentdata2013 data, does education of father matter in their children's academic performance (rank)?

4. Using studentdata2013 data, does having electricity at home (electricity) improve students' academic performance (rank)?

5. Using studentdata2013 data, does mother involvement improve academic performance (rank) of their children?

6. Using studentdata2013 data, does father involvement improve academic performance (rank) of their children?

7. Please do not simply paste your outputs, but also add your answer in writing as well.



Note: **, one-tailed test tests just one direction of a relationship; whereas two-tailed test tests both directions (your p-value will need to be divided by two). One-tailed test is more powerful than a two-tailed test, because one-tailed test does not need to be divided--it's just a test for one direction. If you know the direction of your relationship (e.g., females perform better than males), then use a one-tailed test. If you do not know the direction, then use the two-tailed test. If you use a two-tailed test, and want to get a one-tailed result, then just divide the p-value of the two-tailed p-value by 2. In your ttest gpa, by(sexstud) above, your two-tailed test p-value is 0.0000 (the one in the middle). If you divide it by 2, it is still 0.0000 (the one on the right side). To get another one in the left side, you use 1-.0000, and it's 1.0000. To keep it simple, we will just use a two-tailed p-value throughout the class. Also note that usually a two-tailed test is shown by default in any statistical outputs.     
  

Variable Manipulation and Computation and Reliability Check

This week we are going to learn how to manipulate, compute, and check the reliability of your variables. You will learn how to re-code the response of your variables and compute to a new variable of your interest.

RE-CODING 

Why re-coding?

There are a few reasons why you need to re-code your variables. First of all if your variable is unreasonably skewed or is not normally distributed and you want to make the response to that variable less skewed so that your results would be enhanced based on proportional response to your variable. For example, let's take a look at this variable--number of absence-- in this dataset (file name: studentdata2008). Students responded to this variable by writing down their total number of absences since the beginning of their current academic year. The response ranges from 0 to more than one times. You would do the command tab to get the detail list of each response of "absent" variable. Here is how it looks like:

tab absent

As you can see from the above table, only very few students were absent more than 6 times. So your data were skewed toward 0-5 times. When you look at the Skewness value of this variable, it's 2.49 and Kurtosis it's 11.15 which indicate highly skewed (see the short and sweet description of Skewness and Kurtosis here for more information). In this case, you would re-code this variable by combining those who were absent more than 6 times into one group, calling it as "more than 6 times". You leave 0-5 as it it--don't touch them. To recode this variable, use this command: recode absent (0=0)(1=1)(2=2)(3=3)(4=4)(5=5)(6/25=6). Here is how it looks like:

recode absent (0=0)(1=1)(2=2)(3=3)(4=4)(5=5)(6/25=6)

That is what you get based on that recode command above. Next, tab absent again, and you will see that the response 6-25 was combined. here is how it looks like:

tab absent 

Now your variable absent looks like it's normally distributed. The Skewness was reduced to 0.57 and Kurtosis to 1.88. The rule of thumb of a normally distributed variable would be a skewness of 1 and lower (nearer to zero is better) and Kurtosis of lower than 3.

So how did you do to get the values of Skewness and Kurtosis of the absent variable? 

Type command summary (or sum) of absent variable by requesting detail (or simply d for shortcut). Here is how it looks like:

sum absent, detail

So there you have the values of Skewness and Kurtosis. The values indicate that your variable absent looks normally distributed. Below is a screenshot of how Skewness and Kurtosis are mentioned in a journal article (click here for the full article in the American Journal on Addictions):

Another reason for you to recode a variable is when you want to group the response into a category. Again, this is purpose driven--very subjective. Now look at the variable "age". Ages of respondents range from 10-19 years old. If your purpose is to group them into a 5-year range, then you will have two groups: 10-14 and 15-19. You would follow the same as the above procedures. Here is how it looks like when you tab age:

tab age 

Now let's do recoding of age:

recode age (10/14=1)(15/19=2) 
or 
recode age (min/14=1) (15/max=2) 

I would recommend you to label this age variable as its values have been recoded so that you can still remember when you come back to the data in the future. Use the command: label var age "5-year range of age, 1=10-14 and 2=15-19"; description inside the quotation mark can be anything you want to call. It's for you to remember what it is you recoded. Here is how it looks like after you label it:

label var age "5-year range of age, 1=10-14 and 2=15-19"

tab age

There is another way to label values (1 or 2 for the age above) and have it displayed in the output table like this one above. So instead of showing 1 and 2 and look at the label of the variable in the red circle, you can have it shown 10-14 or 15-19 instead. Here is how you do it:

label define age1 1 10_14yrs 2 15_19yrs

label values age age1 

The "age1" can be anything you want to call it, and have need something for you to define the value label. Another important thing to remember is that please be careful about the "hyphenate" and "dash" as Stata is sensitive to the hyphenate one. Stata would treat it as "from this to that." So if it is a label you want to remember on your own, use "dash". For the example above, if you write "10-14yrs, then Stata would not be running, and it shows an error message saying that it's "invalid syntax."

GENERATING NEW VARIABLES 

You always want to retain your original variables before you recode because there is a chance that you may want to come back to those variables again. You never know. If you do not generate a new one, then after you recode it, you can never recall it back. I recommend that you always generate a new variable that is equal to the one you want to work on. A good example would be the variables that we used above: absent and age. You always want to retain these variables and recode the ones that you generate for current use. Generating a variable can be done easily with the command: generate or gen for short. Now let's look at the variables absent again and generate a new one of it. A new variable that you generated (or created) can be called anything you would like to (but no spacing). I myself prefer to use rc adding to the new variable being generated so that I know that it is recoded. So for the absent variable, the newly generated one would be called "absent_rc". So here is how it looks like:

gen absent_rc = absent 

And again, you should label this variable so that you won't forget what it is called when you come back later. I assume that by now you know how to label your variables. So show me how you would do it!. After you have done it, the new label will appear in the yellow highlight part above. Please note that when you generate a new variable that is equivalent to your old one, the new one must be placed first, right after "gen" command. Remember, you generate new variable to be equal to the old one, if that helps you memorize.

Now that you have generate your new absent variable, you can use that one to do the recoding. Simple!

--------

Command "gen" can be used to generate (or convert) values of your variables as well. For example, for your variable "dob" (date of birth in actual year), the response was in actual year. It looks like this by using tab command:

... but you want to make this variable to actual age (let's say in 2014, how old your participants are). First of you need to call this new variable that you want to generate into actual age. It is up to you what to call, but I would call it as "dob_age". You can generate dob into year by using this one straight command: gen dob_age=(2014 - dob). [Note: it's 2014 minus dob]:

gen dob_age=(2014 - dob) 

Now your dob variable has been converted into actual age, instead of year.

Let's keep it simple for now about the use of gen command. There are many more functions that gen command can give you. For more information on gen, the UCLA website is useful (here is the link).

COMPUTE NEW VARIABLES

Computation to a new variable can be done when you have several variables that you want to average them to a single variable. For example, in your Happiness Survey data (access to the data here), there are 8 variables that were used to measure physical problems of the participants. So by combining or averaging the 8 variables together, you create a new single variable or a scale that measures physical problem. You use command "gen" or "egen" to average these 8 variables: gen physical_problem = (Psleep + Pache + Phead + Peat + Ptired + Pfam + Pworry + Pfocus)/8. Here is how it looks like:

gen physical_problem = (Psleep + Pache + Phead + Peat + Ptired + Pfam + Pworry + Pfocus)/8

Now you have created/computed/generated a new variable or a new measure for physical health. And again, you should label this variable so that you won't forget what it is later. I assume that by now you know how to label your variable.

Another way to generate this physical problem variable, you can use "egen" command. It looks like this:

egen physical_problem = rmean (Psleep - Pfocus) 

That should also generate/compute your physical problem measure.

RELIABILITY CHECK

Before you create a measure such as the one above, the physical problem one, you may want to check how reliable the measure is. In other words, how each item is correlated with one another. This is called inter-item reliability. We use Cronbach's alpha to evaluate the reliability of a measure you are trying to create. As a rule of thumb, a Cronbach's alpha of above 0.70 is considered a good and 0.80 up is considered to be highly reliable. Let's look at the physical problem measure and how reliable it is. We can use the command: alpha. Here is how it looks like:

alpha Psleep - Pfocus

What it shows here is the alpha = 0.7772 (or .78). We can say that the physical problem measure is reliable. A value below .70 is usually not so welcomed by peer-reviewed journal.

This is an example of how this part of analysis is presented in a peer-reviewed journal.

Source: Plunkett, S. W., Henry, C. S., Robinson, L. C., Behnke, A., & Falcon III, P. C. (2007). Adolescent perceptions of parental behaviors, adolescent self-esteem, and adolescent depressed mood. Journal of Child and Family Studies, 16(6), 760-772.

PRACTICE IN CLASS

Now let's practice this in class as part of our class activities. Use this data for this purpose.
We will use the variables gpa, absent, and age1skol to answer the following questions:

1. Do students who have 3 times and above of absence tend to start their first grade later than those who have the number of absence of 2 times and below (hint: group absent into two groups)?
2. Do students who have GPA of above average (5 and above) tend to start their first grade earlier than those who have a GPA of lower than the average (below 5)?
3. Make sure that after  you group the responses, you label the newly created variables so that you remember what they are.


PRACTICE ON YOUR OWN

Using studentdata2008 and do the following:

1. Create a new variable of sexstud (and call it as gender)
2. Label the values of your newly created variable gender. Your task is to change from 0 to female, and 1 to male (hint: use label define and label values commands).
3. Currently, your gpa variable is a continuous variable (ranging from as low as 2.05-9.63). 
1. Your task is to create a new gpa variable into four groups, 
2. Then calculate percentages of the four groups. 
3. After that, please label to the values of the groups. 
4. Then, find out how each of these GPA groups is different by gender (e.g., who perform better? Male or Female?).
4. Recode the variable numstud (e.g., number of students) into whatever number of group you think would makes sense practically in the real world. 
1. Then, recode variable absent (e.g., the number of absent) into whatever number of group you think makes sense practically. 
2. Label to the values of the groups of absence and the group of number of students. 
3. Your final task is to run a cross-tabulation between number of students and number of absent. Do those coming from a larger class size have more number of absence? 
5. Use, Happiness Survey, and create a measure called Happiness
1. How reliable is this measure? 
2. Are men more likely to be reporting more happiness than women? 
3. Are those reporting higher level of happiness more likely to do well academically (e.g., using gpa variable)? 

Good luck! 

Descriptive Data Analysis

This week we are going to learn about conducting basic data analysis such as tabulation, cross tabulation, mean, standard deviation, median, mode, minimum, and maximum. You can use the Happiness Survey data to conduct the analysis.

Tabulation

In Stata, command “tab” will give you three things: freq. (or frequency), Percent, and Cumulative Percent. You use tab when your variables are categorical (e.g., gender, political affiliation, ethnicity etc.). Below is an example of how “tab” command looks like with e.g., Gender:

It should be noted that this data coded 1 as Male and 2 as female. So what this result shows is that we have 8 males (or 33.33%) and 16 females (or 66.67%) in your data. Forget about the Cum. column as you will not use it as much (if you want to learn more about it, here is the link). Sometimes you may forget what you coded for 1 and 2. I would recommend relabeling the variable Gender. You would type: label var Gender "gender: 1=male & 2=female". Here how it looks like after you entered that command:

Now you can see that 1 is male and 2 is female right in the results table.

You can also use tab for continuous variables as well if you want to know the number/percentage of a specific value. For example, in your Happiness Survey data, we have a question that asks number of years of education of the participants. The response to this question ranges from at least 12 years of education to higher. Below is an example of tab Edu:

tab Edu

Based on the above table, I want to know how many respondents who have 20 years of education. What it shows you here is that 17.39% (N=4) of your respondents have 20 years of education. It gives you the details of each year of education reported. You can also see that there is one person whose education is 23 years. Therefore, depending on your need of information, you can use tab command for either categorical or continuous variables, but you may find yourself using it more for categorical variables.

Cross-Tabulation 

Cross-tabulation gives you results of frequency and percentage of two groups of variables, such as gender (male vs. female) and pet owning (owning vs. not owning). In Stata, you can do this by using the command "tab" and the two variables right after it: "tab Gender Pet". Here is how it looks like:

tab Gender Pet

Based on the above table, you can see that females (coded as 2, N=12) tend to own more pet (coded as 1 for owning a pet, and 0 not owning one) than males do.

You can also request for percentage as well for easy read. You can add "column" or "col", "cell" and/or "row", right after the comma: "tab Gender Pet, col row cell". Here is how it looks like:

tab Gender Pet, col row cell

Here is how you interpret the result above:

From a row of Gender: among all of the female (coded as 2) who responded to the survey, 75% own a pet.

From a column of Pet: among all of those who responded owning a pet (coded as 1), 80% are females.

From a cell of Pet: among all of the respondents, 52.17% are females owning a pet.

Summary 

In Stata, the command "summary" or "sum" in short gives you Obs (your total number of response or your total number of participants), Mean (or your average score), Stad. Dev. (standard deviation), Min (minimum) and Max (maximum). You use "sum" command basically when you want to know the average of a variable (such as income, age, or likert scale response). Your variables should be continuous, ordinal, interval, or ratio (for more info of scale measurements, you can read via this link). Let's try to find the average or mean of GPA based on your Happiness Survey:

sum GPA

What you got here is the mean value of GPA which is 3.79. It seems that everyone is doing so well as you can see that the deviation is pretty small (SD=0.20). The values of Min and Max tell you the lowest GPA and highest GPA. We covered this as well in your previous class on data cleaning. Later, you will learn how to compare means (of GPA) with different groups or categories (such as gender or ethnicity). Techniques used for mean comparisons are t-test and ANOVA (One way Analysis of Variance). For now, let's just look into mean comparisons using a very basic technique using the command: tab Gender, sum (GPA). This command will give you result of the average GPA across gender. In other words, your question would be "Is there any differences in academic performance among male and female?" Here is how it looks like:

tab Gender, sum (GPA)

The table above tells you that female students tend to perform better than their male counterparts. The average GPA for female is 3.834 and for male 3.7.

Mode

Mode is the number that appears to be repeatedly more often than other numbers. As far as I know, Stata does not have a command for Mode. I may have missed it, but you all can help me search for it. But do not worry about it as Mode is not commonly used. Just to give you a whole picture of how to find mode in your Stata report, I use the Edu variable as an example. You use the command "tab" to give you a list of all the responses. Type tab Edu and you will get the following look:

tab Edu

Based on the table above, the 17 years of education appears to be the most common number reported by the participants--6 people reported that they have 17 years of education. So 17 is your mode value.

Median 

Media is the value in the middle. It is useful for some variables such as income, as mean may be misleading if a few people earn way too high or too low. According to 2010 U.S. Census, the income is reported using median. An except below is how it is written (full link to the report is here):

For the purpose of illustration, let's use the variable Edu from our Happiness survey, and try to find out what is the median (we do not have income variable though). In Stata, the median can be generated via the use of "sum" but with an additional request by using "detail" option after comma. Here is how it looks like: "sum Edu, detail". Detail can be "d" as a shortcut.

sum Edu, detail 

Based on the above table, the median is the 50%, which is 18 years of education. 

Practice on your own

1. What is the average of number of countries have the respondents been to? 
2. Are there any differences in the number of countries visited based on gender? 
3. Did those who vote during the election have higher GPA than those who did not vote? 
4. Did those who vote during the election like to drink wine than those who did not vote? 
5. Create two questions on your own and run the analysis. 

Good luck! 

Data Cleaning and Editing

This week we will learn about data cleaning and editing. Data cleaning is a procedure to examine if the values of your variables are entered correctly. As you recall from the last week's class, we do data coding in order to make data (participants' responses) more manageable, in a numeric pattern so that statistical software such as Stata, SPSS, or Excel can read, hence allowing you to analyze them. So how do you go about checking if the values of your variables were entered correctly? We can check for accuracy to some extent but not entirely. For example, in your Happiness Survey data (code file), if we were to investigate if the values of variable "political affiliation" were entered correctly, we use the command: "summary" or "sum" in short, of that variable that was coded as “Pol”. The values of this variable range from 1-3 in which 1 indicates Democrat, 2 Republican, and 3 None. When you use the command “sum” it will give you Obs (your number of your respondents), Mean (or the average), Std. Dev. (standard deviation), Min (minimum) and Max (maximum).  So here how it looks like in Stata:  

Note that the possible values of Pol are 1-3, but what it shows you here is Min 1 and Max 4. So there is something wrong with the data that we entered; specifically, the value 4 should not be in the data. So the next step is to check to find out the number 4 based on the ID associated with this number. Now, we are going to use the command "tabulation" or "tab" in short. So we type "tab Pol" in the command box. Here how it looks like:

tab Pol 

Now what we see is that there are 6 respondents that have the value 4. And you know right away that Gail may have made a mistake when she entered the data with these 6 respondents. So we need to check the IDs of these 6 people. Once we know the IDs, then we can go back to your paper questionnaire. This is why we have to always ID your questionnaire before you enter the data, so that we can always go back to the original source. To find out who are these 6 respondents, we use the command: "tab". So now we "tab ID" with enforced condition only for the variable Pol that has the value of 4. The conditional command is "if". So here how it looks like with the conditional command: "tab ID if Pol==4". Note that the equal sign is double, and variables in STATA are case sensitive. Here is how the output looks like: 

tab ID if Pol==4

Now you know which questionnaire to look into. So if you have the questionnaires in front of you, you can look them up with the above IDs which are: 1, 5, 6, 7, 9, 14. Then, the next step is to fix it using the command "edit". Other conditional command will be used as well such as "|". This "|" tells Stata to select certain number of ID you would like obtain. Here, we want to obtain IDs: 1, 5, 6, 7, 9, and 14, only for Pol equal to 4. Here is how you should type in your command box: "edit Pol if (ID==1 | ID==5 | ID==6 | ID==7 | ID==9 | ID==14)". Note that we use parenthesis right after "if" so Stata knows that you want to request 1 and 5 and 6 and so on. You can also do it one at a time. For example, "edit Pol if ID==1", "edit Pol if ID==5" and so on. Either way that you are comfortable with. So here is how it looks like after you type, "edit Pol if (ID==1 | ID==5 | ID==6 | ID==7 | ID==9 | ID==14)" in your command box: 

edit Pol if (ID==1 | ID==5 | ID==6 | ID==7 | ID==9 | ID==14)

Now Stata gives you all the IDs that you requested that has the value 4 for Pol. Now you can go ahead and replace the value that you found in your paper questionnaire for Pol variable, right in above Window. 

PRACTICE ON YOUR OWN

Now it is your turn to practice on your own. To do this, please download the Excel file HERE. I changed some values in it for practice purpose. Then do the following things: 

1. Click on File

2. Import

3. Excel spreadsheet

4. Browse to the Excel file that you just downloaded from the CourseSite then Open 

5. Check on the box that says: Import first row as variable names 

6. Ok 

Here is what you are supposed to do. I have purposefully selected three variables for you to work on: 

1-Wine (Do you drink wine?). The response is 0 for No and 1 for Yes. So it is between 0 and 1. 

2-Hincred (I am incredibly happy). The response is 1-5 in which 1 is Less True and 5 is More True. 

3-Pfocus (I have difficulty concentrating). The response is 0-3 in which 0 is Never and 3 is Always. 

Your task is to find out if these three variables contain any values that are entered by mistakes. For example, you know that the variable Wine contains just 0 and 1, so the values that are larger than 1 indicates mistake and that is your task to find that out. More specifically, you what you will need to show me is the IDs with the values that were mistakenly entered. Here is exactly what I want from you: 

1-Wine, the IDs are: ..........................

2-Hincred, the IDs are: ......................

3-Pfocus, the IDs are: ........................

I look forward for your results. 

Good Luck!